푸리에 분석
1822년 프랑스의 수학자 Joseph Fourier는 주기적인 파동운동에서 수학적 규칙을 찾아냈습니다.
아주 복잡한 주기적 파동운동까지도 간단한 사인파들로 나눌 수 있었습니다. 그는 모든 주기적 파동을 여러 진동수에 다른 진폭의 사인파의 성분들로 나눌 수 있다는 사실을 발견하였습니다. 이와 같은 수학적 작업을 Fourier 분석이라고 부릅니다.
각도가 변화하면, 빨간 사인 선분의 길이도 변화합니다. 아래 그림의 맨 아래쪽 그림은, 그 길이의 변화를 그래프로 그린 것입니다.
각도 0도에서는 Sin값이 0이고, 즉, 빨간 수직선의 길이가 0 이고, 90도 각도에서는 1이 됩니다. 180도 각도에서는 다시 0이 됩니다.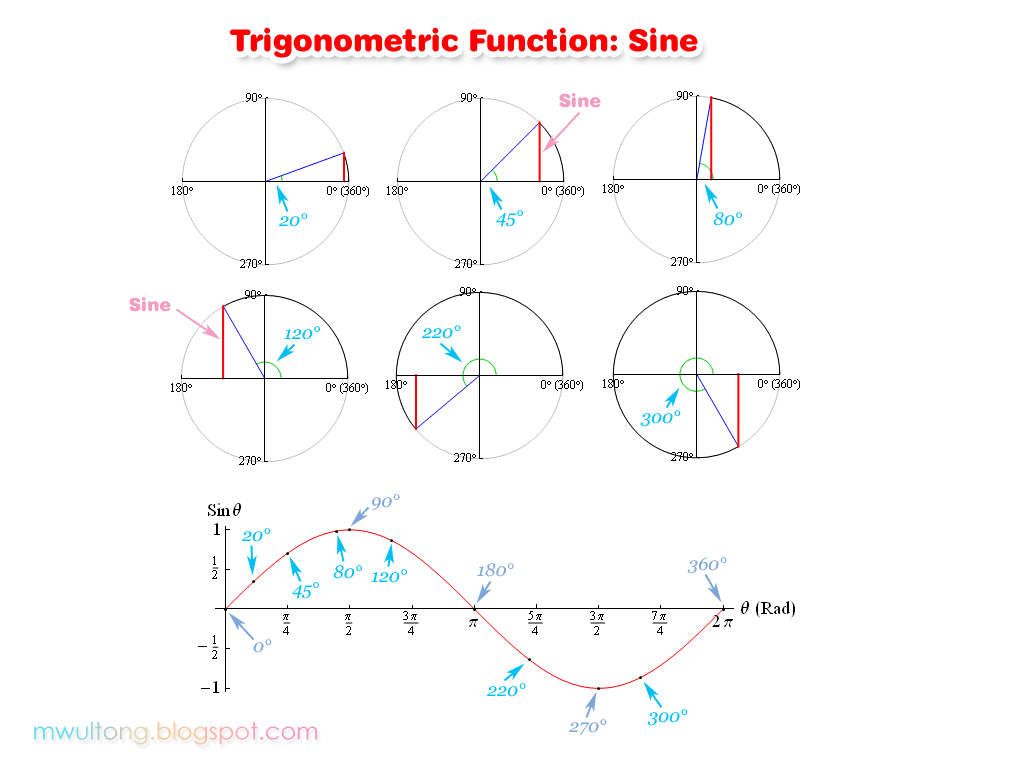
사인함수 개념 차트
사인함수에 입력하는 각도는 보통의 360도 각도가 아니라, 라디안(Rad) 단위여야 합니다. 그러나 위의 원 그래프들은 이해를 돕기 위해 360도 각도 단위를 붙여 놓았습니다.
위의 동그란 그래프들은 "단위 원(Unit Circle)"입니다. 단위원이란 반지름이 1 인 원입니다. 삼각함수에서는 반지름이 1인 원, 즉 단위원을 기준으로 삼습니다.
'컴퓨터이야기' 카테고리의 다른 글
| openface 설치하기 (0) | 2017.11.01 |
|---|---|
| [펌]오일러공식 (0) | 2017.10.20 |
| [펌]공분산 (0) | 2017.09.17 |
| 회귀분석 (0) | 2017.05.15 |
| 데이타 과학자 - 조시 윌스 (0) | 2017.04.20 |